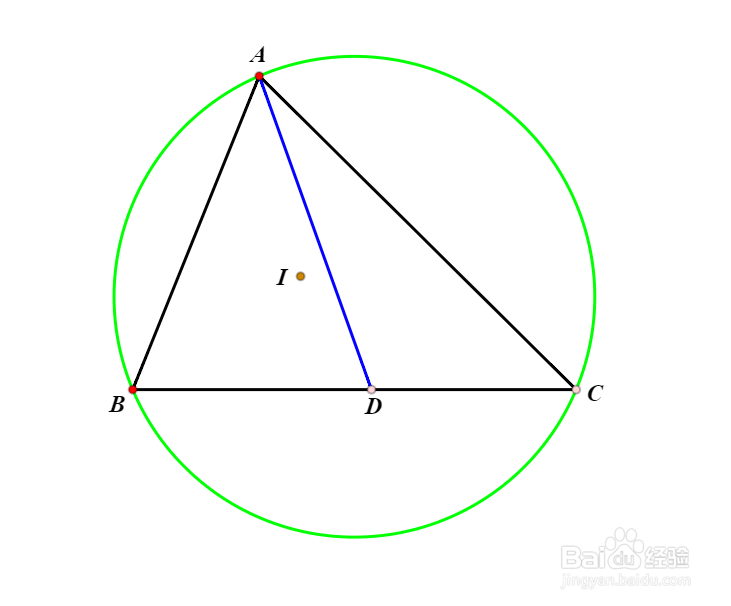
1、作△ABC的内切圆圆心I。
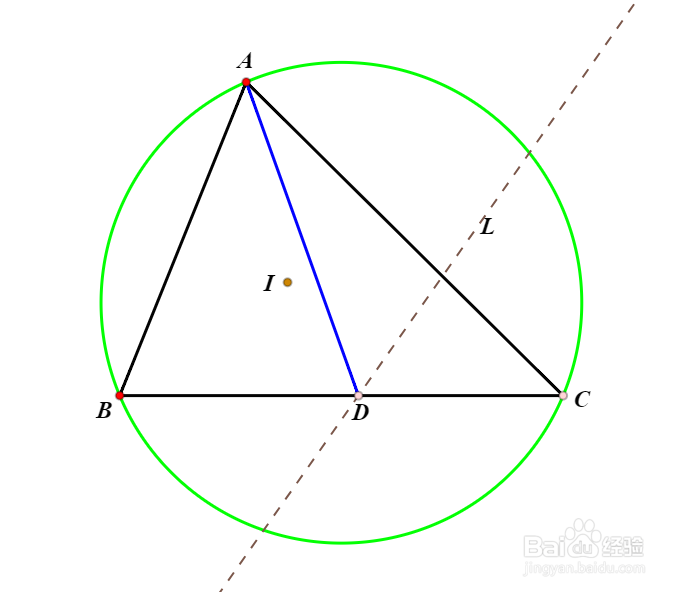
2、作∠ADC的角平分线L。
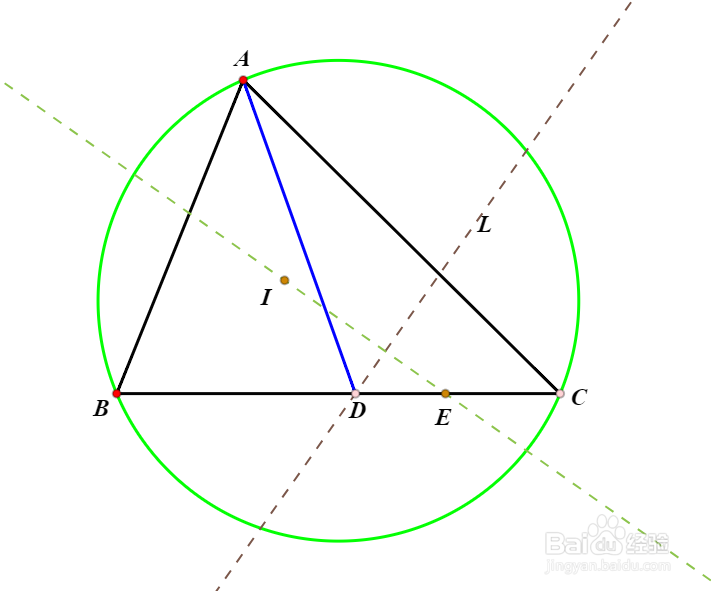
3、过I作L的垂线,与线段CD交于点E。
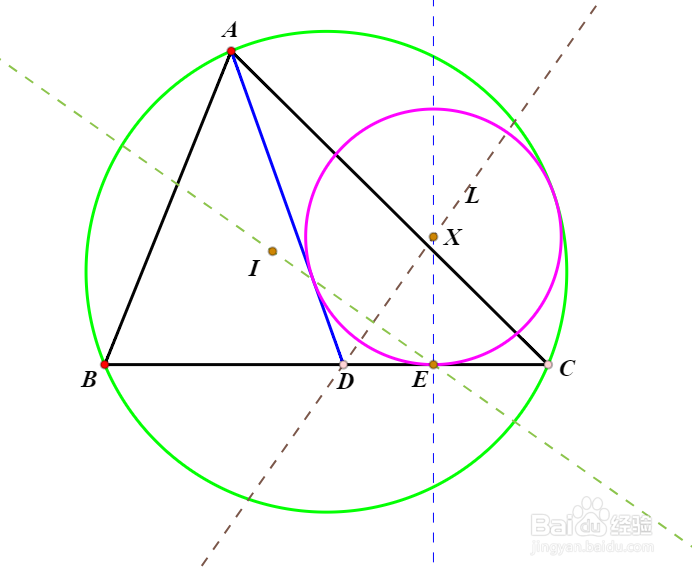
4、过E作CD的垂线,与直线L交于点X。这就是圆X的圆心。

5、作圆X,半径是XE。
1、Sawayama引理:
设圆X与AD切于F那么E、F、I三点共线。
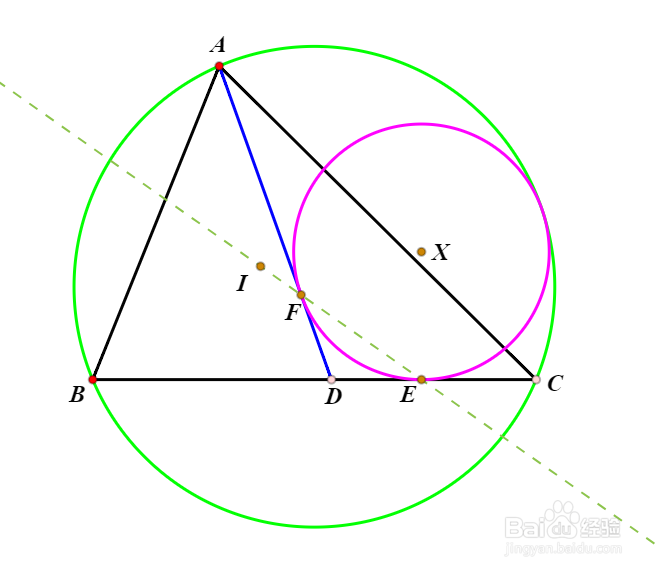
2、Thébault定理:
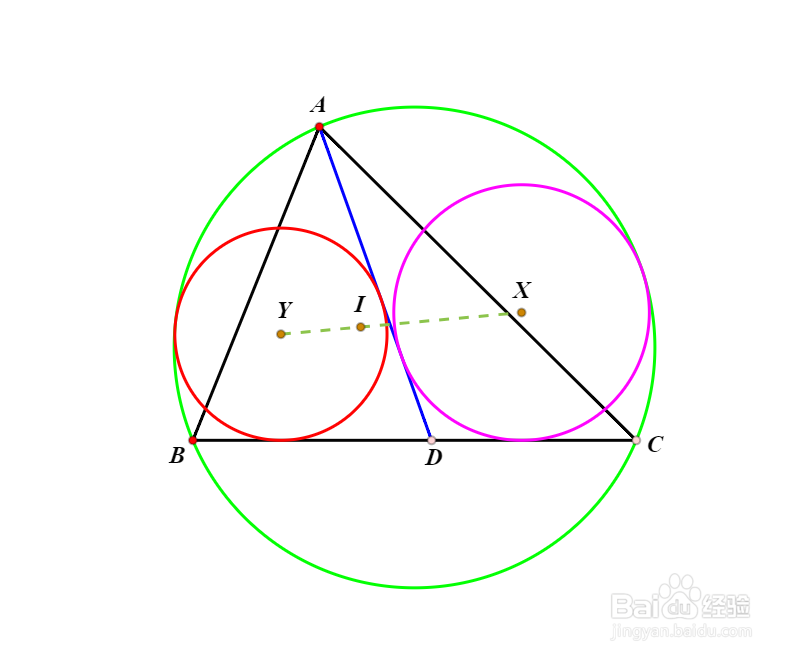
如下图,圆X与线段AD、CD、△ABC外接圆相切,圆Y与线段AD、BD、△ABC外接圆相切,I是△ABC的内切圆圆心,那么X、Y、I共线。
时间:2026-02-13 22:35:07
1、作△ABC的内切圆圆心I。

2、作∠ADC的角平分线L。

3、过I作L的垂线,与线段CD交于点E。

4、过E作CD的垂线,与直线L交于点X。这就是圆X的圆心。

5、作圆X,半径是XE。

1、Sawayama引理:
设圆X与AD切于F那么E、F、I三点共线。

2、Thébault定理:
如下图,圆X与线段AD、CD、△ABC外接圆相切,圆Y与线段AD、BD、△ABC外接圆相切,I是△ABC的内切圆圆心,那么X、Y、I共线。

