不在必修部分,在选修1-1第三章以及选修2-2第一章。
微积分的创立是数学发展的里程碑,它的发展及广泛应用,开创了向近代数学过渡的新时期,它为研究变量与函数提供了重要的方法和手段。导数的概念是微积分的核心概念之一,它有极其丰富的实际背景和广泛的应用。
在本模块中,学生将通过大量实例,经历由平均变化率到瞬时变化率的过程,刻画现实问题,理解导数的含义,体会导数的思想及其内涵;应用导数探索函数的单调、极值等性质及其在实际中的应用,感受导数在解决数学问题和实际问题中的作用,体会微积分的产生对人类文化发展的价值。
扩展资料:
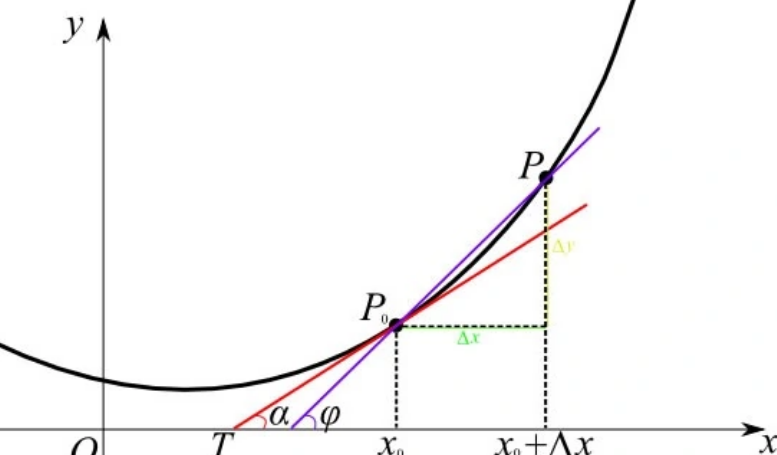
导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话,函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中,物体的位移对于时间的导数就是物体的瞬时速度。
不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在,则称其在这一点可导,否则称为不可导。然而,可导的函数一定连续;不连续的函数一定不可导。
