1、第一步首先我们,设f(x)=arctan x, 今将给出f(n)(x)的一种求法。如图1所示。下一步其中,我们权且引入虚数 i 以便将有理分式进行分拆。接下来就将有如图2所示。
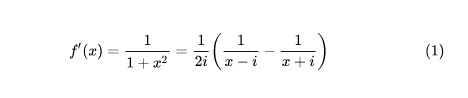
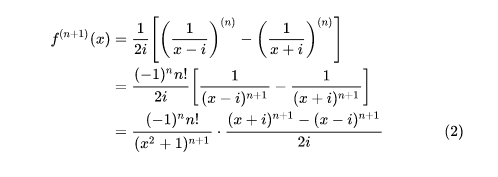
2、下一步 这个式子中仍含有 i 直接这样保留着是不行的,需要设法消去。考虑利用Newton二项式定理,如图所示。
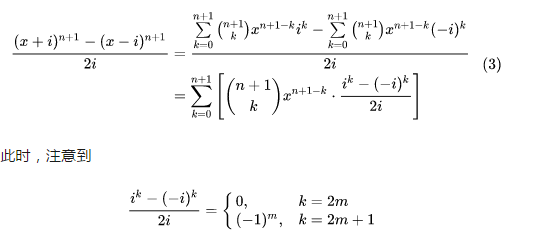
3、下一步 这表明上一步(3)之末式求和号下仅剩 k 取小于 n 的正奇数时的诸项,该事实可以记作,如图所示。
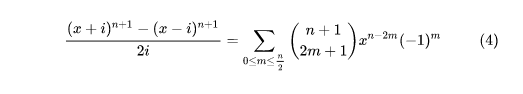
4、下一步 于是得出,图1。最后一步 容易验证上一步(5)对 n=0 也成立,于是将 n—1 作为 n 代入,即得 图2所示。
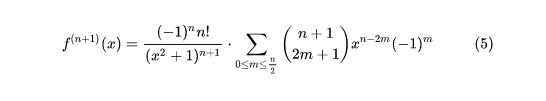
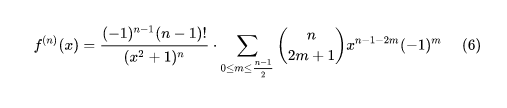
1、设f(x)=arctan x, 今将给出f(n)(x)的一种求法。其中,我们权且引入虚数 i 以便将有理分式进行分拆。接下来就将有。
2、这个式子中仍含有 i 直接这样保留着是不行的,需要设法消去。考虑利用Newton二项式定理。
3、表明上一步(3)之末式求和号下仅剩 k 取小于 n 的正奇数时的诸项,该事实可以记作,得出后,容易验证上一步(5)对 n=0 也成立,于是将 n—1 作为 n 代入,即得
