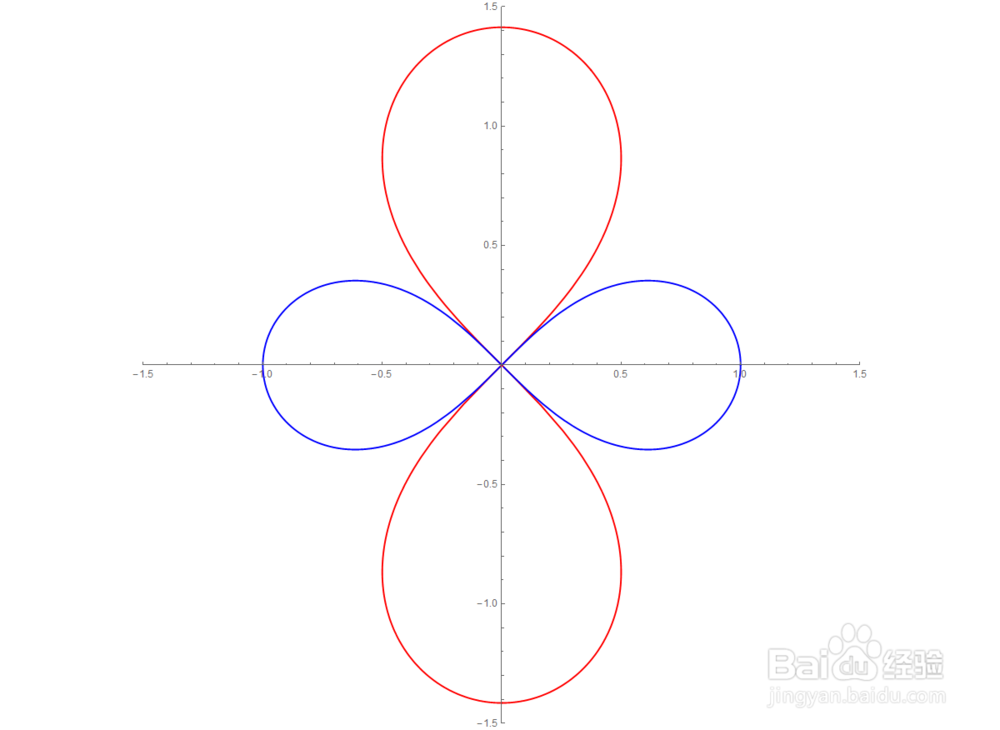
1、双纽线的极坐标方程是:
ρ=Sqrt[Cos[2t]]
图中红色曲线的参数方程是:
{(Sqrt[2] Sin[t] + Sin[2 t])/(3 + 2 Sqrt[2] Cos[t]),
-1 - (Sqrt[2] Cos[t] + Cos[2 t])/(3 + 2 Sqrt[2] Cos[t])}
本文,就来证明,这两个曲线都是双纽线。
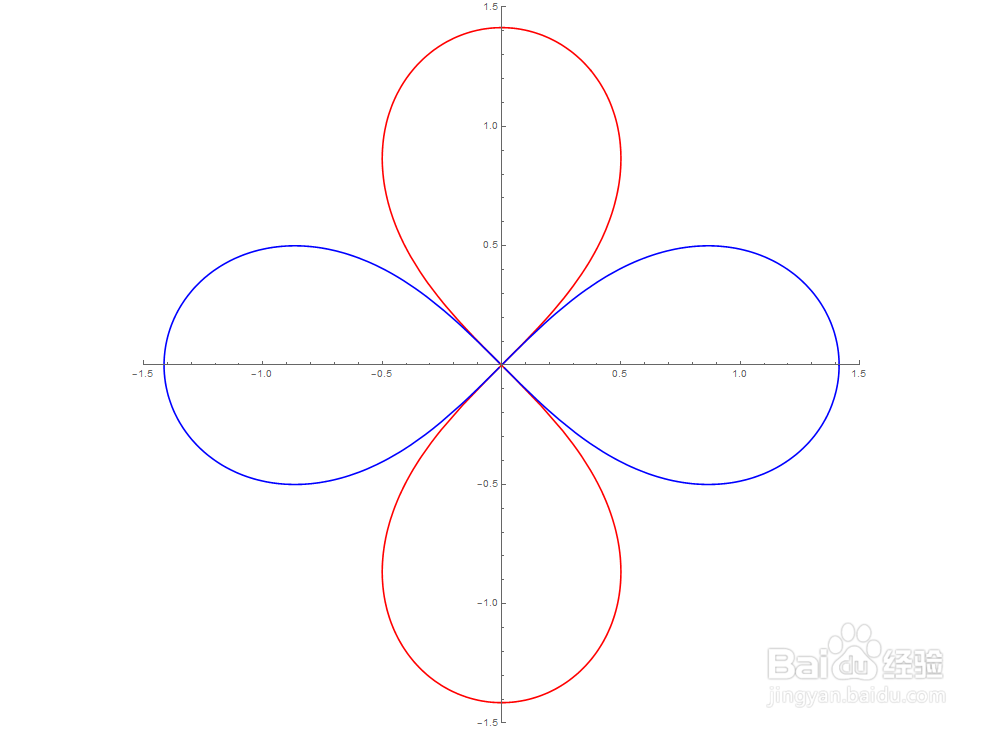
2、把双纽线按比例放大:
ρ=Sqrt[2 Cos[2 t]]
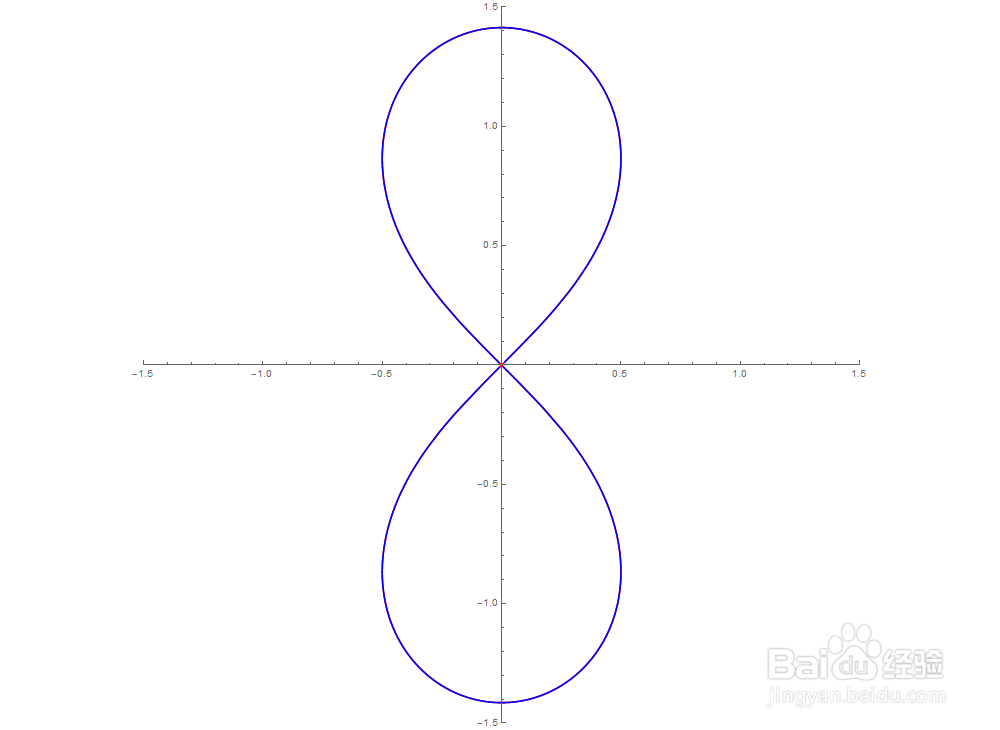
3、再把双纽线旋转90°:
ρ=Sqrt[2 Cos[2 t + Pi]]
与红色曲线重合了,至少看起来是如此。
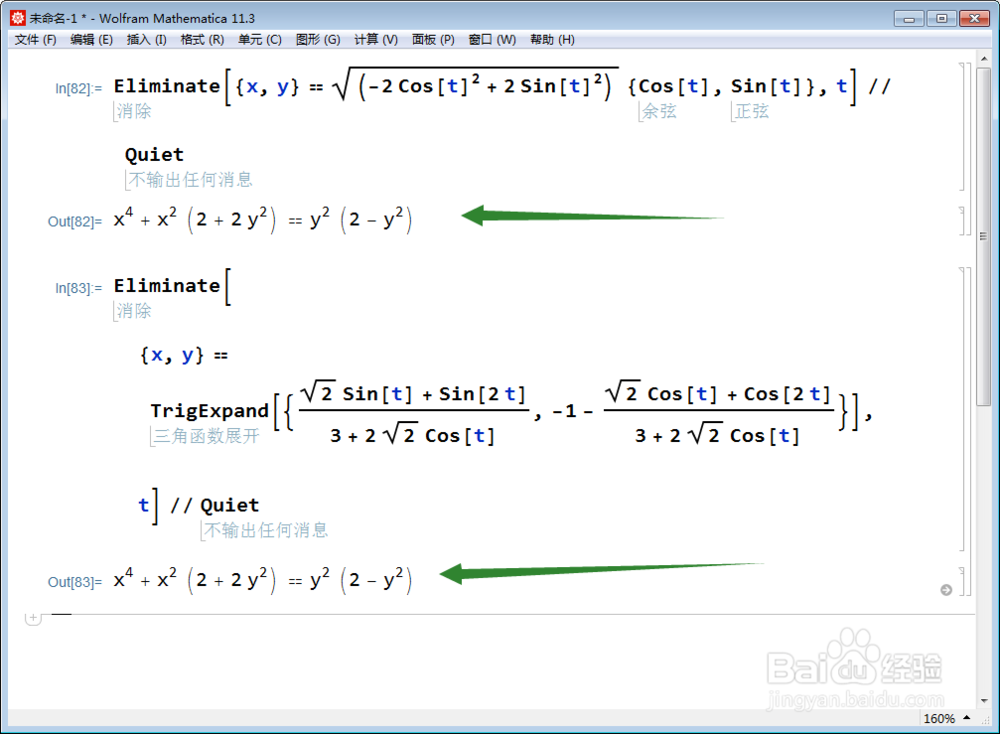
4、要想验证这两个曲线完全重合,就需要它们的隐函数方程一样。
双纽线的隐函数方程是,可以通过消去参数来实现,但为什么消不去呢?
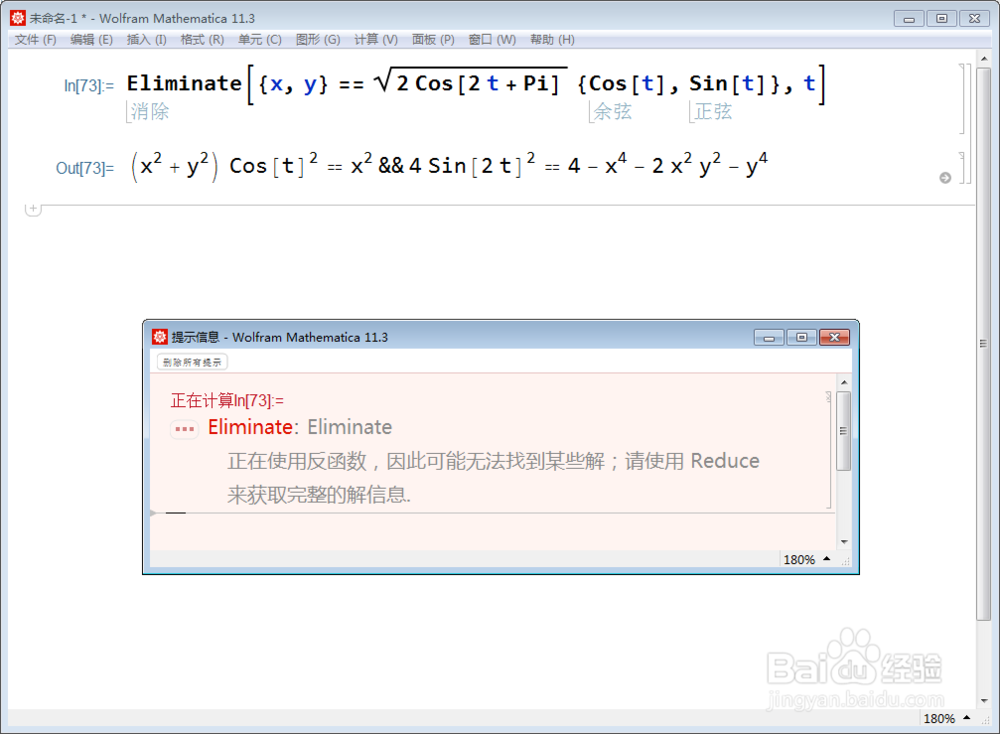
5、把三角函数的倍角全部展开,再消参数,就可以成功:

6、把红色曲线也消去参数;
明显,二者的参数方程一样,所以,红色曲线也是双纽线。
把x和y换为-x和-y,方程式不变,表示双纽线是中心对称图形。