1、 本文主要介绍复合函数y=(x-1)^3的定义域、值域、单调性、凸凹性及极限等性质,并通过导数知识计算函数的单调区间,同时简要画出函数的示意图。
2、因为y=(x-1)^3,可知函数为幂函数的复合函数,根据函数特征,自变量x可以取任意实数,所以函数的定义域为:(-∞,+∞)。

3、通过函数的二阶导数,解析函数的凸凹区间。

4、 二阶导数,是原函数导数的导数,将原函数进行二次求导。一般的,函数y=f(x)的导数y'=f'(x)仍然是x的函数,则y'=f'(x)的导数叫作函数y=f(x)的二阶导数。
5、如果当x趋近于x0(或者无穷大)时,函数f(x)的值无限接近于一个确定的常数A,那么就说A是函数f(x)在x趋近于x0(或者无穷大)时的极限。
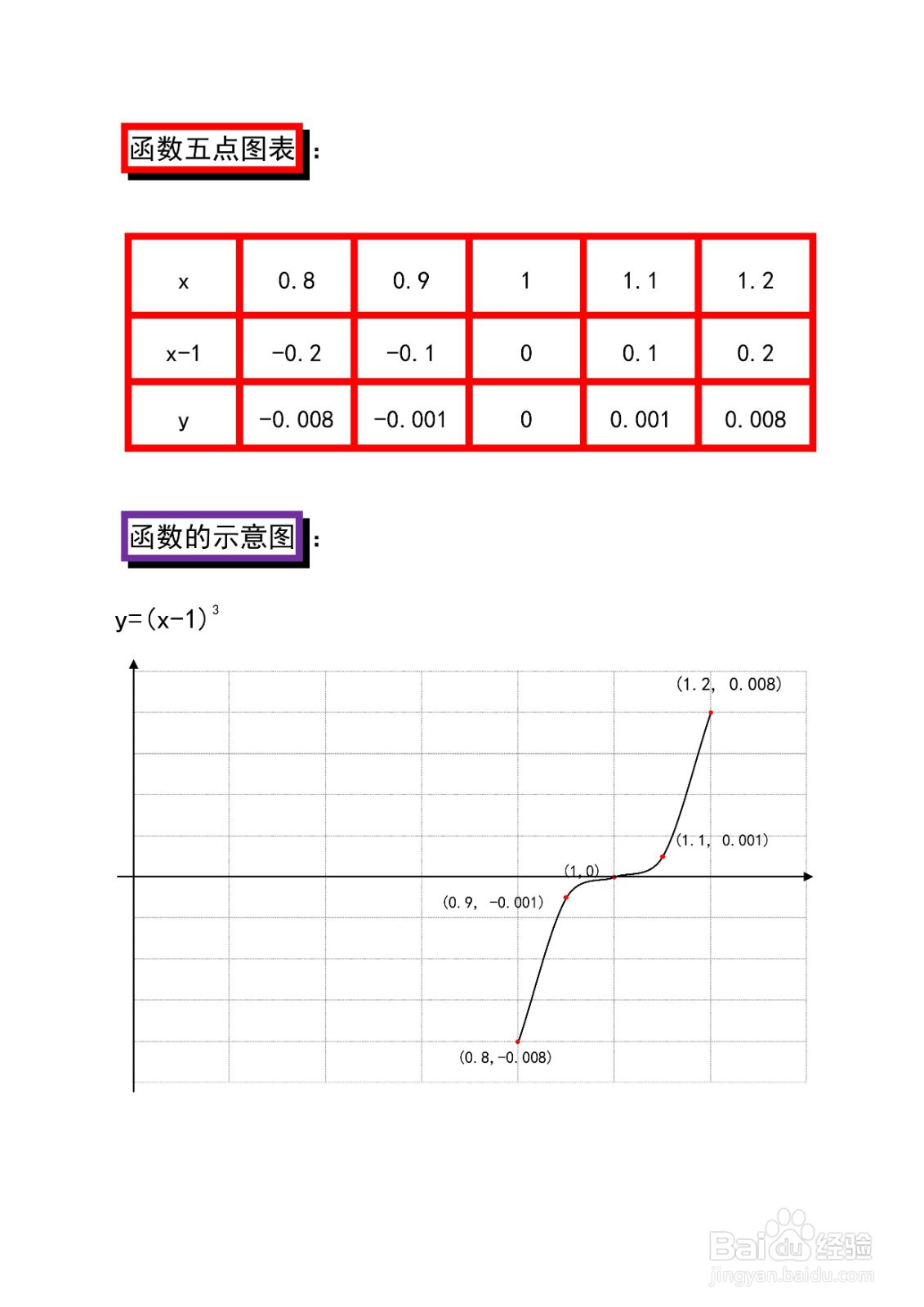
6、函数部分点解析表,以及函数的示意图如下所示。