詹森不等式是以丹麦数学家约翰·詹森(Johan Jensen)命名。它给出积分的凸函数值和凸函数的积分值间的关系。
琴生(Jensen)不等式(也称为詹森不等式),使用时注意前提、等号成立辞包条件。
我们可以推导出低耍其他一些著名不等式,比如幂平均不等式、杨格不救摸佛等式(Young Inequality),赫尔德不等式(H ölder Inequality),闵可夫斯基不等式(Minkowski Inequality)。
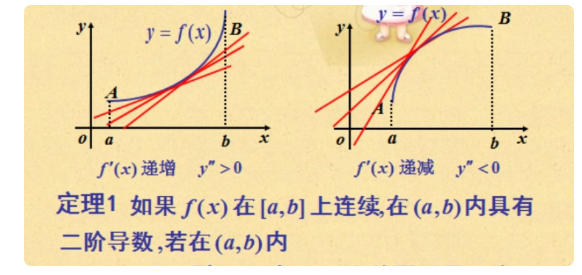
关于琴生不等式的结论:
如果f(x)二阶可导,而且f''(x)≥0,那么f(x)是下凸函数(凸函数)。
如果f(x)二阶可导,而且f''(x)≤0,那么f(x)是上凸函数(凹函数)。
公式应用:(x1^t+x2^t+...+xn^t)/n>=((x1+x2+...+xn)/n)^t,(t>1时);(x1^t+x2^t+...+xn^t)/n>=((x1+x2+...+xn)/n)^t,(0<t<1时);取f(x) = x^t。((x1+x2+...+xn)/n)^n>=x1*x2*...*xn,取f(x)=log(x)。
