1、 下面我们具体看一个例题,看看如何利用点到直线的距离的几何意义,求解函数的最值问题的。
例题:求下图1所示函数的最大值、最小值,题目如下图所示:

2、 接下来我们对原函数进行变形处理,具体变形步骤如下图所示,首先需要对函数进行适当的变形,使变形后的函数满足点到直线的距离公式,这个过程就是点到直线距离公式的配凑过程。

3、 然后我们对点(x,(4-(x-2)^2)^(1/2))作分析,把它变成参数方程,则有x0=t,y0=(4-(t-2)^2)^(1/2)。因为(x0-2)^2+y0^2=(t-2)^2+4-(t-2)^2=4,显然x0,y0满足以(2,0)点为圆心,半径为2的圆,且是上半圆,因为y0>0的。
我们画出直线方程和满足x0,y0的原方程图像,具体图像如下图所示,非常简单,直线方程时一条直线,还有一个以(2,0)点为圆心,半径为2的圆的上半圆。
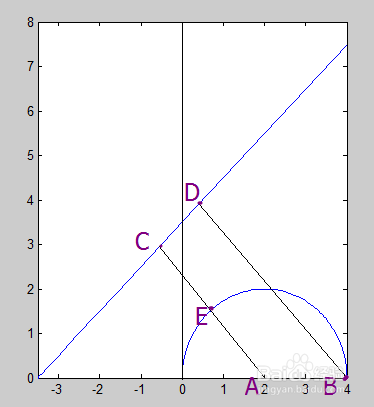
4、 画出图形后,数形结合,在图上过圆心A作直线的垂线,交直线于C点,交圆于E点,在过圆最右端点B作直线的垂线,交直线于D,则很明显圆上点到直线的最小距离是CE,最大距离是BD,再次利用点距离距离公式,计算出CE、BD的大小,即可求得原函数的最值。计算过程如下图所示:

5、 上面我们求出了圆上点到直线的最大最小值,分别为BD、CE长度,将这两个值代入原函数的变形表达式中,可得到函数的最大、最小值。具体如下所示:

