1、把抛物线迭代映射,写为如下的自定义函数:
f[x_, n_] := Floor[3.5*(10^n)* (1 - x) x]/(10.^n)
这样,既考虑了抛物线映射的迭代过程,又考虑了不同精度的结果。
其中,n是正整数,表示每一步都精确到小数点后n位数。
当n=1的时候,只保留小数点后一位数:
n = 1;
xx = NestList[f[#, n] &, N[1/Pi, n], 100]
这个时候,迭代过程迅速收敛。

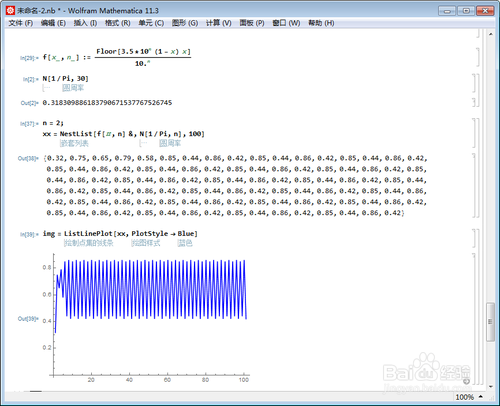
2、n=2,保留小数点后两位数字:
n = 2;
xx = NestList[f[#, n] &, N[1/Pi, n], 100]
第六步之后,开始进入循环状态。
3、n=3,保留小数点后三位有效数字,则在第17步之后,才出现循环状态:

4、n=4,也是在第17步之后出现循环状态:
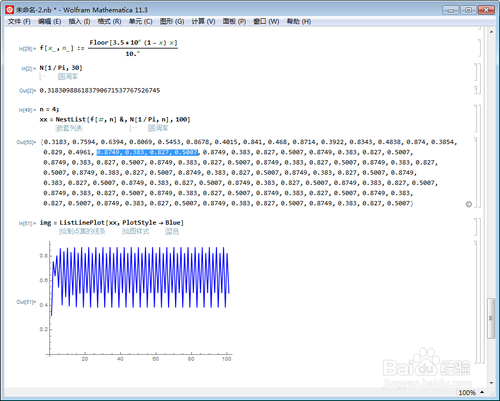
5、n=5,在第21步之后出现循环:

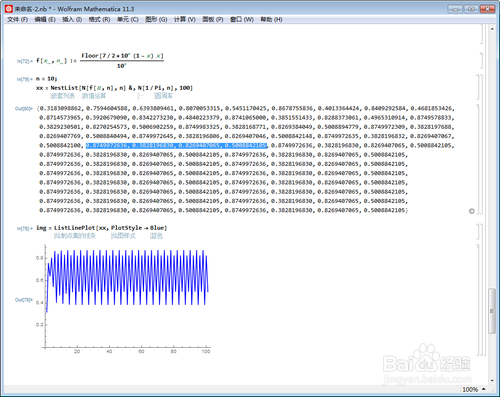
6、n=10,保留小数点后10位有效数字:
f[x_, n_] := Floor[7/2*10^n (1 - x) x]/10^n
n = 10;
xx = NestList[N[f[#, n], n] &, N[1/Pi, n], 100]
在第37步之后才出现循环状态。